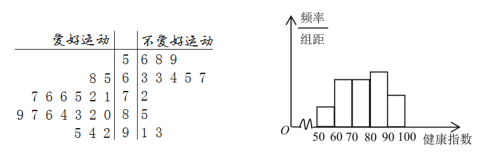
附: 。
| | | | | | | |
| | | | | | | |
| 身体状况好 | 身体状况一般 | 总计 | |
| 爱好运动 |
|
|
|
| 不爱好运动 |
|
|
|
| 总计 |
|
| |