江西省南昌市七校2018-2019学年高二下学期理数期末考试...

参考数据： ， ）

参照附表，得到的正确结论是   

附：由公式算得：

附表：

已知随机变量 且 ， ，则a与b的值为（ ）

对于表中数据，现给出以下拟合曲线，其中拟合程度最好的是   

证明思路：

图1中白色区域面积等于右图中白色区域面积；

图1中阴影区域的面积为ac+bd ， 图2中，设 ，图2阴影区域的面积可表示为 用含a ， b ， c ， d ， 的式子表示 ；

由图中阴影面积相等，即可导出不等式 当且仅当a ， b ， c ， d满足条件时，等号成立．

（Ⅰ）求展开式中各项二项式系数的和；

（Ⅱ）求展开式中中间项．

（Ⅰ） ；

（Ⅱ） .

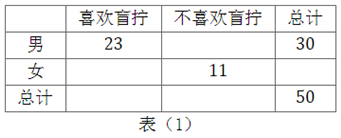
（Ⅰ）将表 补充完整，并判断能否在犯错误的概率不超过 的前提下认为是否喜欢盲拧与性别有关？

（Ⅱ）现从表 中成功完成时间在 和 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录，求2人成功完成时间恰好在同一组内的概率．

附参考公式及数据： ，其中 ．

（Ⅰ）求证 ；

（Ⅱ）若 平面 ．

①求二面角 的大小；

②在棱PC上存在点M ， 满足 ，使得直线AM与平面PBC所成的角为 ，求 的值．

将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立．

（Ⅰ）求在未来3年里，至多1年污水排放量 的概率；

（Ⅱ）该河流的污水排放对沿河的经济影响如下：当 时，没有影响；当 时，经济损失为10万元；当 时，经济损失为60万元 为减少损失，现有三种应对方案：

方案一：防治350吨的污水排放，每年需要防治费 万元；

方案二：防治310吨的污水排放，每年需要防治费2万元；

方案三：不采取措施．

试比较上述三种方案，哪种方案好，并请说明理由．

根据上表数据统计，可知考试成绩落在 之间的频率为 ．

（Ⅰ）求m、n的值；

（Ⅱ）已知本欢质检中的数学测试成绩 ，其中 近似为样本的平均数， 近似为样本方差 ，若该市有4万考生，试估计数学成绩介于 分的人数； 以各组的区间的中点值代表该组的取值 Ⅲ 现按分层抽样的方法从成绩在 以及 之间的学生中随机抽取12人，再从这12人中随机抽取4人进行试卷分析，记被抽取的4人中成绩在 之间的人数为X ， 求X的分布列以及期望 ．

参考数据：若 ，则 ， ， ．