甲:若 , 则在BC上存在2个点P,使
与
相似;
乙:若 , 则
的最大值为
①;②
存在最大值为
;③
存在最小值为
;④点P运动的路径长为
. 其中,正确的是( )
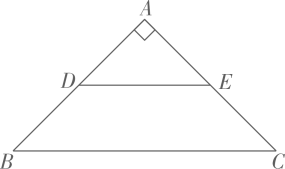
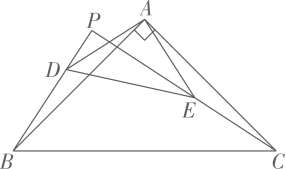
甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
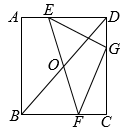
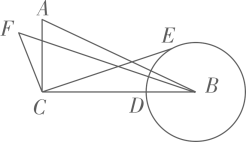
嘉淇的想法是把和
转移到某处,并使它们“接在一起”,然后利用“两点之间,线段最短”尝试探索,并成功解决了问题.以下是她的探索思路,请你按要求补充具体解题过程.
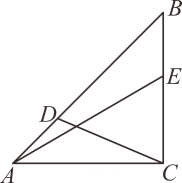
①请你运用尺规作图(保留作图痕迹,不用给出证明),作出 , 并连接
;
②求证: .
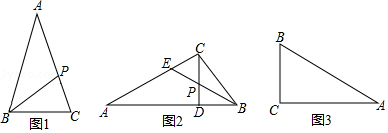
为了探究线段和
之间的数量关系,可先将图形位置特殊化,将
绕点A旋转,使
重合,如图2,易知
和
之间的数量关系为;
继续将绕点A旋转,使
与
重合时,如图3,(1)中线段
之间的数量关系仍然成立,请加以证明.
根据上述探究的经验,我们回到一般情况,如图1,在其他条件不变的情况下,上述的结论还成立吗?请说明你的理由.
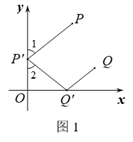
①若点与点
关于
双对合,求
的取值范围;
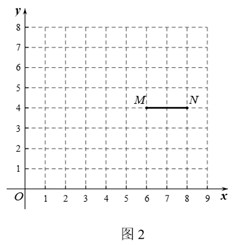
②当点运动时,若
上存在一点与
上任意一点关于
双对合,直接写出点
的横坐标
的取值范围.
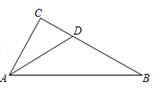
①在点 中,线段
的“等幂点”是 ▲ ;
②若存在等腰 是线段
的“等幂三角形”,求点B的坐标;
【探究】用边共相似点探究三角形的形状
【探究2】用内共相似点探究三角形的内角关系
【探究】探究直角三角形共相似点的个数
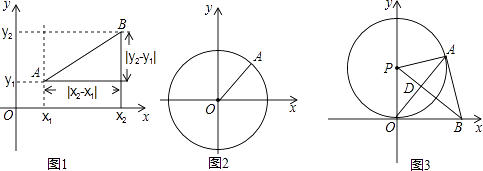
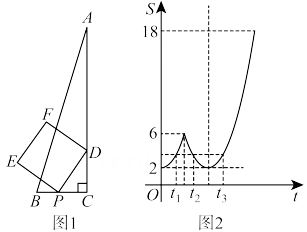
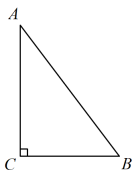
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= ,AB=c=2,那么
=
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=
=
的关系.
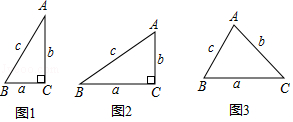
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
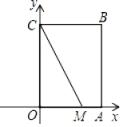
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB= .
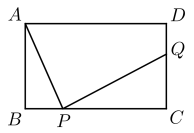
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
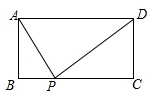
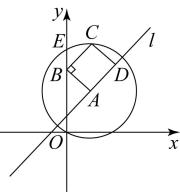
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.