新疆乌鲁木齐地区2019届高三理数第二次质量监测试卷

更新时间：2019-06-12 浏览次数：257 类型：高考模拟

一、单选题

1. 设集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 已知复数z= $\text{[math]}$ （i是虚数单位），则复数z的虚部为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 图象关于原点对称且在定义域内单调递增的函数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 若实数x，y满足 $\text{[math]}$ ，则函数 $\text{[math]}$ 的最大值为 $\text{[math]}$ $\text{[math]}$

A . 12 B . $\text{[math]}$ C . 3 D . 15

答案解析收藏纠错 + 选题
5. 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异” $\text{[math]}$ 其中“幂”即是截面积，“势”是几何体的高，意思是两等高立方体，若在每一等高处的截面积都相等，则两立方体的体积相等，已知某不规则几何体与如图所示的几何体满足“幂势同”，则该不规则几何体的体积为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ． $\text{[math]}$

答案解析收藏纠错 + 选题
6. 已知实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则a，b，c的大小关系是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019·南昌模拟) 如图所示算法框图，当输入的 $\text{[math]}$ 为1时，输出的结果为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
8. 已知 $\text{[math]}$ ， $\text{[math]}$ 是双曲线 $\text{[math]}$ 的焦点，以 $\text{[math]}$ 为直径的圆与一条渐近线交于P，Q两点，则 $\text{[math]}$ 的面积为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
9. 若关于x的方程 $\text{[math]}$ 在区间 $\text{[math]}$ 上有两个根 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则实数m的取值范围是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 设 $\text{[math]}$ ， $\text{[math]}$ 分别是椭圆 $\text{[math]}$ 的左、右焦点，直线l过 $\text{[math]}$ 交椭圆C于A，B两点，交y轴于C点，若满足 $\text{[math]}$ 且 $\text{[math]}$ ，则椭圆的离心率为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. 已知A，B，C为球O的球面上的三个定点， $\text{[math]}$ ， $\text{[math]}$ ，P为球O的球面上的动点，记三棱锥p一ABC的体积为 $\text{[math]}$ ，三棱銋O一ABC的体积为 $\text{[math]}$ ，若 $\text{[math]}$ 的最大值为3，则球O的表面积为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. f（x）的定义域是（0，+∞），其导函数为f′（x），若f′（x）- $\text{[math]}$ =1-lnx，且f（e）=e²（其中e是自然对数的底数），则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. 在平面直角坐标系xOy中，若直线 $\text{[math]}$ 与曲线 $\text{[math]}$ b， $\text{[math]}$ 相切于点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. 如图，在圆内接四边形ABCD中，已知对角线BD为圆的直径， $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题

16. 记公差不为零的等差数列{a_n}的前n项和为S_n ，已知a₁=2，a₄是a₂与a₈的等比中项．
（Ⅰ）求数列{a_n}的通项公式；

（Ⅱ）求数列{ $\text{[math]}$ }的前n项和T_n ．

答案解析收藏纠错 + 选题
17. 如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠DAB=60°，PD=4，M为PD的中点，E为AM的中点，点F在线段PB上，且PF=3FB．

（Ⅰ）求证EF∥平面ABCD；

（Ⅱ）若平面PDC⊥底面ABCD，且PD⊥DC，求平面PAD与平面PBC所成锐二面角的余弦值．

答案解析收藏纠错 + 选题

18. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近 $\text{[math]}$ 个月广告投入量 $\text{[math]}$ （单位：万元）和收益 $\text{[math]}$ （单位：万元）的数据如下表：

月份	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
广告投入量	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
收益	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

他们分别用两种模型① $\text{[math]}$ ，② $\text{[math]}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

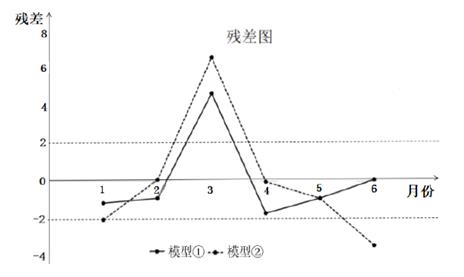
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $\text{[math]}$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $\text{[math]}$ 时，该模型收益的预报值是多少？

附：对于一组数据 $\text{[math]}$ ， $\text{[math]}$ ，……， $\text{[math]}$ ，其回归直线 $\text{[math]}$ 的斜率和截距的最小二乘估计分别为：

 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题

19. 已知拋物线C： $\text{[math]}$ 经过点 $\text{[math]}$ ，其焦点为F，M为抛物线上除了原点外的任一点，过M的直线l与x轴、y轴分别交于A，B两点．
$\text{[math]}$ Ⅰ $\text{[math]}$ 求抛物线C的方程以及焦点坐标；

$\text{[math]}$ Ⅱ $\text{[math]}$ 若 $\text{[math]}$ 与 $\text{[math]}$ 的面积相等，证明直线l与抛物线C相切．

答案解析收藏纠错 + 选题
20. 已知函数f（x）=e^x+ $\text{[math]}$ （其中e是自然对数的底数）．
（Ⅰ）当t=0时，求f（x）的最值；

（Ⅱ）若t≠0时，f（x）在（ $\text{[math]}$ ）上的最小值为1，求实数t的取值范围．

答案解析收藏纠错 + 选题
21. 在平面直角坐标系xOy中，曲线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ ， $\text{[math]}$ 为参数 $\text{[math]}$ ，在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ．
$\text{[math]}$ Ⅰ $\text{[math]}$ 写出 $\text{[math]}$ 的普通方程和 $\text{[math]}$ 的直角坐标方程；

$\text{[math]}$ Ⅱ $\text{[math]}$ 若 $\text{[math]}$ 与 $\text{[math]}$ 相交于A，B两点，求 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
22. 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
$\text{[math]}$ Ⅰ $\text{[math]}$ 当 $\text{[math]}$ 时，求不等式 $\text{[math]}$ 的解集；

$\text{[math]}$ Ⅱ $\text{[math]}$ 若关于x的不等式 $\text{[math]}$ 有实数解，求实数a的取值范围．

答案解析收藏纠错 + 选题