19.
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为

、

、

三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
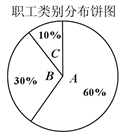
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以( Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.